| Android Adventures - Beginning Bitmap Graphics |
| Written by Mike James | ||||||
| Monday, 27 July 2015 | ||||||
Page 2 of 5
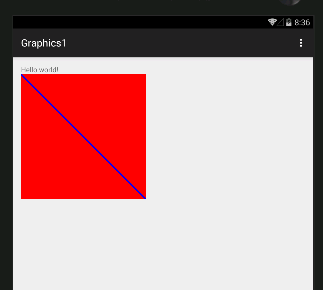
A First GraphicNow we have a Paint object we can draw a line:
This draws a line from 0,0 to 500,500 and as the Bitmap is 500 by 500 pixels this draws a diagonal line across the entire bitmap. Again the numeric values all end in F because the method needs float values - for reasons that will become clear later.
All you have to do now is get to know the different drawing methods provided. Here are a few of the most common. First we need to set the Paint object we created earlier to a FILL style so that we draw solid blocks of color and not just outlines:
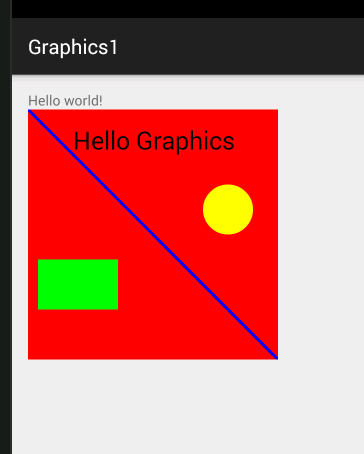
To draw a yellow circle all we need is:
The first two parameters give the position of the center and the third is the circle's radius. To draw a green rectangle:
The first two parameters give the top left hand corner and the next two the bottom right hand corner. Finally some text:
The Paint object has a number of properties that let you set the font and style. In this example we simply set the text size. The drawText method takes a string, the start and end positions of characters in the string that will be displayed and the coordinates of the starting location. If you put this all together and run it you get the very tasteful graphic:
The complete code to create this is:
You can use this to try out other Canvas graphics methods. If is worth pointing out that there is a set of drawBitmap methods that you can use to draw an existing Bitmap onto the Bitmap associated with the Canvas. This might seem like a strange thing to do but it is one of the most useful drawing operations because you can us it to implement simple sprite animation. TransformationsNow we come to one of the more sophisticated options that Canvas offers. Before anything is drawn the coordinates you supply are acted on by a transformation matrix. By default this is set to the identity matrix which leaves the coordinates as they were. However there are a range of transformation methods which modify the transformation matrix:
There are also some methods that let you work directly with the transformation matrix:
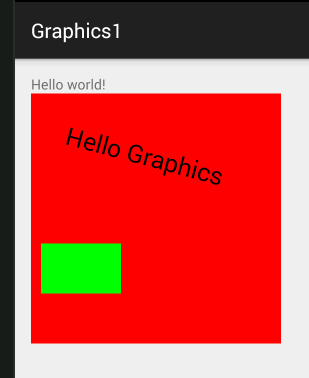
If you know how matrices and transformation matrices work then this will be nothing new to you. If you don't know about transformations and matrices then there are a lot of traps waiting to trip you up. The main one that gets just about everyone at first is that the order in which you do things matter. A translation followed by a rotation isn't the same thing as a rotation followed by a translation. Try it if you don't believe me. Another one is that these transformations change the coordinate system and don't affect anything you have already drawn. They only change what happens when you draw something after the transformation has been applied. For example:
In this case there is a 15 degree rotation after the rectangle has been drawn and before the text is drawn. The result is that the rectangle stays where it was but the text is rotated.
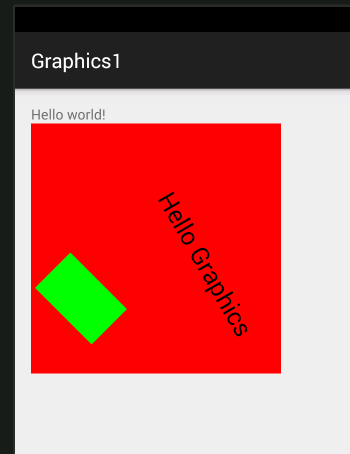
After the rotation everything you draw will be at 15 degrees. Notice that the rotation is about the origin i.e. 0,0 the top left hand corner. If you want to rotate about a different point, usually the center of some object you need to use rotate(d,x,y). For example to rotate the rectangle about it's center you would use:
where 100,350 is the center of the rectangle:
You can also see that the text is now in a different position and not simply rotated about the origin. This is because the 15 degree rotation is added to the 45 degree rotation around the center of the rectangle. To keep your transformations separate and non-interacting you have to remember to return the transformation matrix to the identity after you have changed it to something else. How do you set the matrix back to the identity? You could use
as Matrix() creates an identity matrix by default or you could just use
because passing a Null causes the matrix to be reset. However, needing to make a change to the transformation matrix and then restore the original is such a common operation that Canvas supports:
which saves the current matrix and
which restores the current matrix. For example:
With the save before the first rotate, the restore before the second decouples the two transformations. |
||||||
| Last Updated ( Wednesday, 12 October 2016 ) |