Once you move beyond simple shapes like rectangles, circles and ellipses, the first thing you are likely to encounter is the Bezier curve. In this extract from my book on JavaScript Graphics, we look at what makes a Bezier curve.

Now available as a paperback or ebook from Amazon.

JavaScript Bitmap Graphics
With Canvas

Contents

1. JavaScript Graphics
2. Getting Started With Canvas
3. Drawing Paths
     Extract: Basic Paths
     Extract: SVG Paths
     Extract: Bezier Curves
4. Stroke and Fill
     Extract: Stroke Properties 
     Extract: Fill and Holes
     Extract: Gradient & Pattern Fills
5. Transformations
     Extract: Transformations
     Extract: Custom Coordinates 
     Extract  Graphics State
6. Text
     Extract: Text, Typography & SVG 
     Extract: Unicode
7. Clipping, Compositing and Effects
     Extract: Clipping & Basic Compositing
8. Generating Bitmaps
     Extract:  Introduction To Bitmaps
     Extract :  Animation 
9. WebWorkers & OffscreenCanvas
     Extract: Web Workers
     Extract: OffscreenCanvas
   
10. Bit Manipulation In JavaScript
      Extract: Bit Manipulation
11. Typed Arrays
      Extract: Typed Arrays **NEW!
12. Files, blobs, URLs & Fetch
      Extract: Blobs & Files
      Extract: Read/Writing Local Files
13. Image Processing
      Extract: ImageData
      Extract:The Filter API
    
14. 3D WebGL
      Extract: WebGL 3D
15. 2D WebGL
    Extract: WebGL Convolutions

<ASIN:1871962625>

<ASIN:B07XJQDS4Z>

<ASIN:1871962579>

<ASIN:1871962560>

<ASIN:1871962501>

<ASIN:1871962528>

In book but not included in this extract:

• Paths
• The Default Path Object
• The Rectangle
• Circles and Ellipses
• Ellipse
• The arcTo Function

Bezier Curves

The most sophisticated of the path creation functions are the two Bezier curve functions. A Bezier curve is a smooth curve that you can use to approximate complex curves. They were invented by Pierre Bezier in the 1960 to give Renault cars their smooth curvy bodies. There are different types of Bezier curves with different properties. What is important to realize is that a Bezier curve isn’t an exact shape like a circle or an ellipse. They are generally created by interactive adjustment of their parameters to give a pleasing shape. For example you might interactively adjust a Bezier curve until it was the shape of a face, then another to be the shape of a nose and so on. The big problem with using Bezier curves with Canvas is that you have to specify them in the function call and getting the parameters right can be very tricky. More on how to do this later.

Canvas supports two types of Bezier curves - quadratic and cubic. The names tell you the highest power that occurs in their implementation. Put simply, cubic Bezier curves are potentially wigglier than quadratic Bezier curves. You can achieve the same overall curve using either type, but you might need more quadratic curves to do the job. In most cases the slightly more complicated cubic curve is the better choice.

To specify the curvature of a Bezier curve you need to specify a starting point, a finishing point and a number of control points. A quadratic Bezier curve has a single control point and it acts like an attractor for the curve pulling it towards it. At the start point the curve is tangent to the straight line between it and the control point. The same is true at the end point where the curve is tangent to the line between it and the control point.

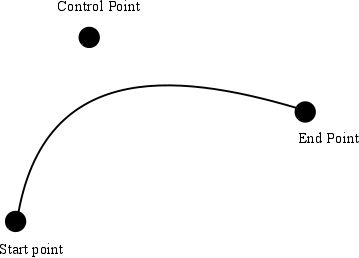
To draw a quadratic Bezier curve you use the quadraticCurveTo function quadraticCurveTo(cpx,cpy,x,y), where the start point is the current point, the end point is x,y, and the control point is cpx,cpy. For example:

path1.moveTo(10,10); 
path1.quadraticCurveTo(200,50,100,100);

draws a curve between 10,10 and 100,100 with a control point at 200,50. You can see the result below with the control point marked as a circle.

The cubic Bezier curve works in much the same way but now there are two control points:

bezierCurveTo(cp1x,cp1y,cp2x,cp2y,x,y);

This draws a cubic curve between the current point and x,y using cp1x,cp1y and cp2x,cp2y as the control points. The action of the control points is more complicated and the first control point affects the curve more close to the start point and the second control point affects it near the end point. The curve is tangent at the start point to the straight line between the start and the first control point, and tangent at the end to the line between the end point and the second control point.

For example:

path1.moveTo(10,10);

path1.bezierCurveTo(200,20,20,200,200,300);

produces a curve with two wiggles:

where again the two control points have been marked with circles.

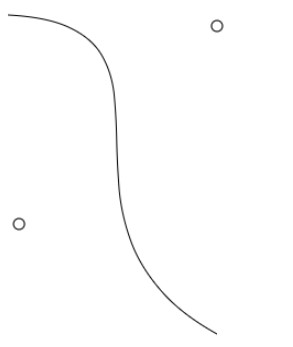
As promised, the cubic Bezier curve can wiggle more than the quadratic. You couldn’t produce this sort of curve with a quadratic because you only have one control point which attracts the curve. With a cubic curve you can “pull” the curve in two different directions.

The big problem with both forms of the Bezier curve is how to specify the control points. You could write a utility that allowed you to draw interactively and so set the control points, but there is a much simpler and better approach. First, however, we need to find out about another way to specify a path.

Omitted from this extract

• Using SVG Paths