| The Trick Of The Mind - Algorithms Binary Search |
| Written by Mike James | |||||
| Tuesday, 07 February 2023 | |||||
Page 2 of 4
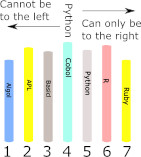
Random Versus NonrandomNow consider an alternative algorithm. As the librarian put the books on the shelf in a random or haphazard order, why not look for a book in the same way? Your algorithm now is to pick a number at random between 1 and N and see if the book is at that location. While Book Not found This is a very simple random algorithm of a type that can be applied to many different types of problem that don’t seem to involve randomness in any way. It may be simple but is it any good? On average, if the book is in the library, you will find the book in N steps, which isn’t as good as half that (N/2) for the linear search and, worst of all, if the book isn’t in the array you could search forever as there is no condition that brings the loop to an end other than finding the book. Of course, in practice you could add a condition that stops the loop after a large number of steps, but this doesn’t guarantee that the book isn’t on a shelf. The reason is that randomness is just that, random, it doesn’t guarantee that you will have examined every shelf location, no matter how many random numbers you generate. Random algorithms are sometimes better than nothing when a more direct deterministic algorithm is so slow that it is impractical. They are an important class of algorithms that are often overlooked. Problem Sorted!Let us suppose that our librarian wasn’t quite a lazy as assumed so far. If the books are placed on the shelves in alphabetical order starting from the left, then there is a much better way to search for a book. If you have not met it before, this algorithm can seem more complex, but it is much more efficient. The first thing to say is that the books are not in order in the usual “library” way of having a shelf with all of the books beginning with A and then a shelf with all the books starting with B and so on. This is a possible way of doing things, but it has its disadvantages which we will return to this later in the discussion of hashing. In this library the books are just put on the shelves one-after-another but in alphabetical order from the left – a long line of books in alphabetical order with no subdivisions. What this means is that you cannot find where the books starting with P are stored on the shelf. Somewhere in the array of locations there is a first book starting P, but you don’t know where. You can’t look at the title of the book you are looking for and go straight to the start of the alphabetical sequence where is might be. All you have is a sorted list with apparently no obvious way to make use of it. However, a little thought reveals that there is a very good way to make use of it. Start your search in the middle of the array of books. Suppose you discover that the book at this location comes earlier in the alphabetical sequence than the book you are looking for then you know that all of the books to the left cannot possibly be candidates for your book because they are all earlier in the sequence than the book in the middle and hence earlier in the sequence than your book. The books on the right of the middle book are the only ones that could be the book you are looking for as they could be earlier, later or equal to the book you are looking for. For example, suppose we only have seven books and we are looking for a book called Python. The middle book, shelf location 4 is Cobol so we know that, because they are in alphabetical order, Python has to be to the right of the middle book. So by looking at the middle location of the shelf we have reduced the number of books to search from N to roughly half the number – 7 to 3. For a single-search step this is quite good!
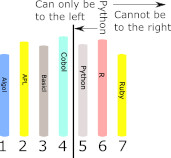
You could start searching for the book in the right-hand portion of the shelf using a linear search, but why not look at the middle location of the right-hand portion? Why not treat the right-hand portion as if it was the entire shelf? After all, what worked for the entire shelf should work for the right-hand half and reduce the part of the shelf that the book can be in by a factor of two again. Pick the middle location of the right-hand portion and compare it to the book you are looking for. If it is later in the sequence then you know that your book has to be in the left-hand half of the overall right-hand portion. Now you have determined that the book you are looking for is in this small section of the shelf which has only a quarter of the locations. In the case of our example you can see that the middle book is R (R is a programming language used in statistics) and this means any Python book has to be to the left. Again we have reduced the search area from 3 to 1. You can continue in this way, halving the possible range that the target book can be in until you either run out of locations or find the book. In the case of our example the next step is a search of just one location and we find the book we are looking for.
This algorithm is called binary search because it divides the range of possible locations by approximately two at each step. In this case we have found the book in three steps where a linear search would have required five steps. This is a small gain, but the gain gets bigger the more books there are to search. For example, if you have 1000 books to search then using linear search on average it takes 500 steps to find the book and 1000 steps to be sure it isn’t present, but it takes only 10 steps to find or not find it using binary search. Binary Search Made PreciseEven though you understand the overall intent of the binary search algorithm, converting it into a precise list of instructions is more difficult than you might think and doing so highlights what programming is really all about. At the moment we have a description of the algorithm that requires the intelligence of a human to implement it. For example, what exactly does “the middle book” actually mean. It is clear that the algorithm is still a good one if the book selected isn’t exactly in the middle. As long as it divides the set of books currently being searched into two roughly equal parts then everything works reasonably well. However, a program has to specify exactly how to find the middle element. It can’t simply say “pick the middle element”. If there are N books then the middle book should be somewhere near the N/2 shelf location. For example, if N is eight then N/2 is four and this might as well be taken to be the middle book – notice that for even N there is no book that divides the set into two equal halves. For N equal to 8 the fourth book has three to its left and four to its right but this doesn’t matter too much to the overall algorithm. If N is odd we have another problem. For example if N is seven N/2 is 3.5 which isn’t a shelf location. We can make it a shelf location by rounding up or rounding down. Rounding up gives four which does divide the set of books into two equal portions. In most computing language rounding up is done using a function called CEIL for ceiling and so CEIL(3.5) is 4. In general we can use CEIL(N/2) to find the middle book of a set of N books. With this we can now write the exact instructions for the first step of our algorithm: Middle = CEIL(N/2)
If shelf(Middle) == target Then Book found
If shelf(Middle) < target Then
search right portion
Else
search left portion
|
|||||
| Last Updated ( Tuesday, 07 February 2023 ) |