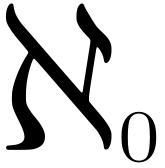| Non-Computable And Other Numbers |
| Written by Mike James | ||||||
| Thursday, 14 March 2019 | ||||||
Page 5 of 5
Pi The Special TranscendentalPi is one of the most fascinating of transcendental numbers because it has so many ways of computing its digits. What formulas can you find that give a good approximation to Pi? Notice that an infinite series for Pi gives an increasingly accurate result as you compute more terms of the series. So if you want the 56th digit of Pi you have to compute all the digits up to the 56th as well as the digit of interest - or do you? There is a remarkable formula - the Bailey–Borwein–Plouffe formula - which can provide the nth binary digit of Pi without having to compute any others. The digits of Pi cannot be random - we compute them rather than throw a dice for them - but they are pseudo random. It is generally said that if you enumerate Pi for long enough then you will eventually find every number you care to specify and if you use a numeric code you will eventually find the any text you specify. So Pi contains the complete works of Shakespeare, or any other text you care to mention; the complete theory of QFT; and the theory of life the universe and everything. However, this hasn't been proved. Any number that contains any sequence if you look for long enough is called normal, and we have never proved that Pi is normal. All of this is pure math but it is also computer science because it is about information, computational complexity and more. The standard theoryNow that we have arrived at these major conclusions it might be worth giving some of the more standard math. Mathematicians say that two sets are equal in size if you can pair up items in one set with the items in the other one-to-one with none left over - they have the same cardinality and this idea works for infinite sets as well as finite ones. All finite enumerable sets have cardinality equal to the number of elements they contain {a,b,c} has cardinality 3. All infinite enumerable sets can be put into one-to-one correspondence and so have the same cardinality which is traditionally called Aleph Zero or enumerable infinity.
Aleph zero the size of the first or countable infinity The set of real numbers i.e. including the irrationals isn't enumerable and is a "bigger" set than an enumerable set - it has cardinality Aleph One and is the infinity of the continuum i.e. the full number line. There are a whole set of increasingly large infinities with cardinality Aleph Two, Three and so on.. And, yes, the set of infinities is thought to be an enumerable infinity - but I don't think anyone has proved the enumerable part as yet. If you want to know more look up transfinite numbers or read The Programmer's Guide To The Transfinite . This is more or less the end of the story but it really is just the beginning. Read some computer science to find out more. A Programmers Guide To Theory
|
||||||
| Last Updated ( Saturday, 16 March 2019 ) |