| Programmer's Guide To Theory - Splitting the Bit |
| Written by Mike James | ||||||||||||||
| Monday, 22 July 2024 | ||||||||||||||
Page 2 of 3
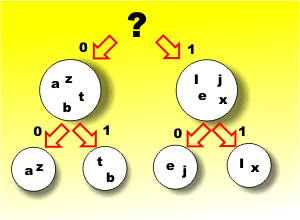
Make it equalIf you have a set of symbols then the most efficient way of using them is to make sure that the average amount of information per symbol is maximized. From our discussion so far, it should now be clear that the way to do this is to ensure that each symbol is used equally often – but how? The answer is to use a code that forces the symbols to occur equally often, even if they don’t want to! Consider the standard alphabet and divide it into two groups of letters so that the probability of a letter belonging to either group is the same, i.e. 0.5. To do this we have to include a mix of likely and not-so-likely letters to get the right probability. With this division of the alphabet we can begin to construct our code by using a 0 to indicate that the letter is in the first group and a 1 to indicate that it is in the second group. Clearly the first bit of our code has an equal chance of being a 0 or a 1 and we can continue on in this way by sub-dividing each of the two groups into equally likely subsets and assigning 0 to one of them and 1 to the other:
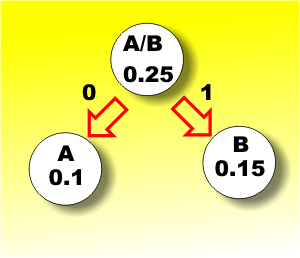
Now when we receive a set of data bits we use them one after another to find which group the letter is in much like a well known “yes/no” question and answer game. Each group is equally likely and hence each symbol used in the code is also equally likely (only 8 letters shown in the diagram). This code was invented by Shannon and Fano and named after them. If you can construct such a code it is optimal in the sense that each symbol in the code carries the maximum amount of information. The problem is that you can’t always divide the set into two equally probable groups – not even approximately! There is a better code. Huffman codingThe optimal code for any set of symbols can be constructed by assigning shorter codes to symbols that are more probable and longer codes to less commonly occurring symbols. The way that this is done is very similar to the binary division used for Shannon-Fano coding, but instead of trying to create groups with equal probability we are trying to put unlikely symbols at the bottom of the “tree”. The way that this works is that we sort the symbols into order of increasing probability and select the two most unlikely symbols and assign these to a 0/1 split in the code. The new group consisting of the pair of symbols is now treated as a single symbol with a probability equal to the sum of the probabilities and the process is repeated. This is called Huffman coding, after its inventor, and it is the optimal code that we have been looking for. For example, suppose we have the five symbols A, B, C, D, E with probabilities 0.1, 0.15, 0.2, 0.25 0.3 respectively:
The first stage groups A and B together because these are the least often occurring symbols. The probability of A or B occurring is 0.25 and now we repeat the process treating A/B as a single symbol:
The first stage of coding
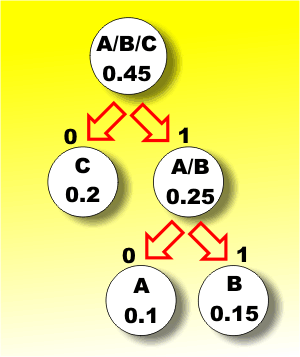
Now the symbols with the smallest probability are C and the A/B pair which gives another split and a combined A/B/C symbol with a probability of 0.45. Notice we could have chosen C and D as the least likely given a different, but just as good, code.
The second stage |
||||||||||||||
| Last Updated ( Monday, 22 July 2024 ) |