Lambda calculus is close to logic and pure maths and it can be difficult to see what it is actually all about in practical terms. So there is a need for a plain-spoken guide suitable for programmers.

A Programmers Guide To Theory

Now available as a paperback and ebook from Amazon.

Contents

1. What Is Computer Science?
   Part I What Is Computable?
2. What Is Computation?
3. The Halting Problem
4. Finite State Machines
   Extract 1: Finite State Machines
5. Practical Grammar
6. Numbers, Infinity and Computation
   Extract 1: Numbers 
   Extract 2: Aleph Zero The First Transfinite
   Extract 3: In Search Of Aleph-One
   Extract 4: Transcendental Numbers
   
7. Kolmogorov Complexity and Randomness
   Extract 1:Kolmogorov Complexity 
8. The Algorithm of Choice
9. Gödel’s Incompleteness Theorem ***NEW!
10. Lambda Calculus
    Part II Bits, Codes and Logic
11. Information Theory 
12. Splitting the Bit 
13. Error Correction 
14. Boolean Logic
    Part III Computational Complexity
15. How Hard Can It Be?
    Extract 1: Where Do The Big Os Come From
16. Recursion
    Extract 1: What Is Recursion
    Extract 2: Why Recursion
17. NP Versus P Algorithms
    Extract 1: NP & Co-NP
    Extract 2: NP Complete

<ASIN:1871962439>

<ASIN:1871962587>

Turing’s approach via a machine model has a great deal of appeal to a programmer and to a computer scientist but, as we have just seen in the previous chapter, mathematicians have also considered what is computable using arguments based on functions, sets and logic. You may also recall that the central tenet of computer science is the Church-Turing thesis and Alonzo Church was a mathematician/logician who tackled computability from a much more abstract point of view. He invented Lambda calculus as a way of investigating what is and what is not computable and this has lately become better known because of the introduction of lambda functions within many computer languages. This has raised the profile of the Lambda calculus so now is a good time to find out what it is all about.

What is computable?

Lambda calculus is an attempt to be precise about what computation actually is. It is a step on from pure logic, but it isn't as easy to understand as the more familiar concept of a Turing machine.

A Turing machine defines the act of computing in terms that we understand at a reasonable practical level - a finite state machine and a single tape that can be read and written. The concept is about the most stripped-down piece of hardware that you can use to compute something. If something isn't Turing computable then it isn't computable by any method we currently know.

Lambda calculus is an alternative to the "hardware" approach of a Turing machine and it too seeks to specify a simple system that is powerful enough to compute anything that can be computed. One way of putting this is that the Lambda calculus is equivalent to a Turing machine and vice versa. This is the Church-Turing thesis - that every function that can be computed can be computed by a Turing Machine or the Lambda calculus. There are a number of alternative formulations of computation but they are all equivalent to a Turing Machine or Lambda calculus.

Lambda calculus started out as an attempt to create a logical foundation for the whole of mathematics, but this project failed due to the paradoxes that are inherent in any such attempt. However, a cut-down version of the idea proved to be a good model for computation.

The basic lambda

The most difficult thing to realize about Lambda calculus is that it is simply a game with symbols. If you think about it all of computation is just this - a game with symbols. Any meaning that you care to put on the symbols may be helpful to your understanding but it isn't necessary for the theory.

In the case of Lambda calculus, first we have the three rules that define what a lambda expression is:

1. Any "variable", e.g. x, is a Lambda Expression, LE

2. If t is a LE then (λx.t) is a LE where x is a variable

3. If t and s are LEs then (t s) is also a LE.

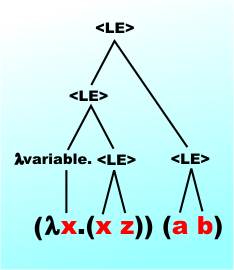
The use of the term "variable" is also a little misleading in that you don't use it to store values such as numbers. It is simply a symbol that you can manipulate. The parentheses are sometimes dropped if the meaning is clear and many definitions leave them out. Rule 2 is called an abstraction and Rule 3 is called an application.

If you prefer we can define a simple grammar for a lambda expression, <LE>:

<LE> → variable | (λ variable. <LE>)|(<LE> <LE>)

Notice that what we have just defined is a simple grammar for a computer language. That really is all it is, as we haven't attempted to supply any meaning or semantics to the lambda expression.

Examples of lambda expressions along with an explanation of their structure:

y Rule 1

x Rule 1 
 (x y) Rule 3

z Rule 1
 (λx.(x z)) Rule 2
 ((λx.(x z))(a b)) Rule 1, 2 and 3

To make sure you follow, let's parse the final example.

The first term is:

(λx. <LE>) 

with

<LE>=(x z)

Of course, x and z are LEs by Rule 1 and the second term is just (a b), which is again an LE by Rule 3. The two terms fit together as an LE, again by Rule 3.

A rough syntax tree is:

The parentheses are a nuisance so we usually work with the following conventions:

1. outermost parentheses are dropped - a b not (a b)
   
   
2. terms are left associative - so a b c means ((a b) c)
   
   
3. the expression following a dot is taken to be as long as possible - λx.x z is taken to mean λx.(x z) not (λx. x) (z)

In practice is it Convention 2 that is most difficult to get used to at first, because it implies that a b c is three separate lambda expressions not one consisting of three symbols. If in doubt add parentheses and notice that grouping of terms does matter as expressed in the basic grammar by the presence of brackets. Without the brackets the grammar is ambiguous. Also notice that the names of the variables don't carry any information. You can change them all in a consistent manner and the lambda expression doesn't change. That is, two lambda expressions that differ only in the names used for the variables are considered to be the same.