| Lottery Ticket Hypothesis - Who Needs Backprop Just Prune |
| Written by Mike James | |||
| Wednesday, 05 February 2020 | |||
|
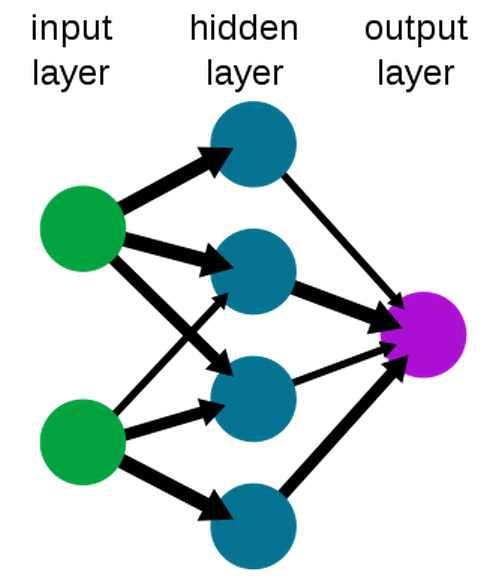
New research suggests that a random neural network may have the same power as a fully trained network and uncovering this is just a matter of pruning the connections. Is this profound? Is this obvious? Does it have implications for real neural networks?
The lottery ticket hypothesis, proposed by Frankle and Carbin in 2018, is a strange idea. It is that inside every random neural network there is a smaller network that, after training, can do as well as the whole network. After spending time exploring this idea, it now seems that this is just a small part of a bigger phenomenon. The hypothesis was extended to: "a sufficiently over-parameterized neural network with random initialization contains a subnetwork that achieves competitive accuracy (with respect to the large trained network), without any training." This has now been proved in a new paper by a small team from the Hebrew University and the Weizmann Institute of Science. If you think about it for a moment this doesn't seem all that amazing as the trick is in the "sufficiently over-parameterized" part. A big network can have millions of parameters and if they are chosen at random then it is highly likely that there will be a sub-network that performs well without being trained. It is not so much the lottery ticket hypothesis as the million dice hypothesis. If you throw a million dice into the air then the chances are you can find a small sub-set that will give you any desired short sequence of outcomes. Practically speaking what this means is that we might be wasting our time using back-prop or gradient descent to train our networks. All we have to do is prune a sufficiently large network to reveal the network we want. Of course, the problem here is how to prune the network. In the paper two pruning methods are compared - pruning entire neurons and pruning individual weights, i.e. connections, and it is proved that pruning the weights is strictly stronger. This too doesn't seem too unlikely as pruning neurons reduces the options we have to sculpt the network favorably. The new results also give us some guidance on how over-parameterized the random network has to be. If the target network has depth L, the random network has to have depth 2L and be polynomial in the width. Basically this gives us some idea how many dice we need to find a given sub-sequence of a given length. These bounds give us a hint that the random network doesn't have to be unfeasibly large to contain the sub-network we are looking for. There are also some nice conclusions you can draw from this. The most interesting is that as you can get any desired network by weight-pruning a random network - weight-pruning is a universal approximator. We already know that a sufficiently large network with two or more layers can approximate any function if trained using gradient descent. It is now obvious that you can do the same job by pruning a bigger random network. Could this be a biologically plausible training method? Biological networks could start out very over parameterized and simply slim down to a network that works by a modified Hebbian learning? Sadly one other conclusion is: "However, as we mentioned previously, our results imply that there is no efficient algorithm for weight-pruning of a random network, by reduction from hardness results on learning neural networks. Hence, weight-pruning is similar to weight-optimization in the following sense: in both methods there exists a good solution, but finding it is computationally hard in the worst case." This is not the dead-end it seems to be because, while this is a difficult task to do analytically, there might be good heuristics that work in practice. The question to be answered is whether these heuristics are better than gradient descent?
More InformationProving the Lottery Ticket Hypothesis: Pruning is All You Need Eran Malach, Gilad Yehudai, Shai Shalev-Shwartz and Ohad Shamir Related ArticlesGoogle Has A Network More Like The Brain How Do Open Source Deep Learning Frameworks Stack Up? Deep Mind's NoisyNet Suggests Random Is Good The Shape Of Classification Space Is Mostly Flat Evolution Is Better Than Backprop? Neural Networks Have A Universal Flaw To be informed about new articles on I Programmer, sign up for our weekly newsletter, subscribe to the RSS feed and follow us on Twitter, Facebook or Linkedin.
Comments
or email your comment to: comments@i-programmer.info |
|||
| Last Updated ( Wednesday, 05 February 2020 ) |