| What Is The Computational Power Of The Universe? |
| Written by Mike James | |||
| Saturday, 25 November 2017 | |||
|
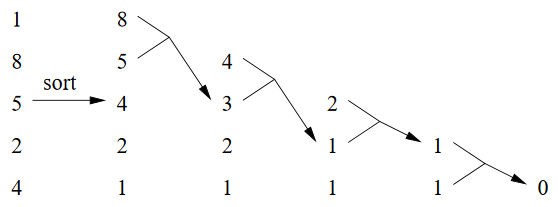
The universe can be viewed as a huge physical computer that has been running for 13.7 billion . The outcome of its program is the way it is. Does the universe actually have the power it needs, or does it need to use clever algorithms? This is a story that needs not just quantum mechanics but quantum field theory, but don't worry you can understand most of what is going on without the details. A team of US researchers, Ning Bao, Raphael Bousso, Stephen Jordan and Brad Lackey, has been puzzling about the fact that the energy density of the vacuum, the cosmological constant, seems to be close to zero. The problem with this observation is that in most of the theories we have there are many ways of creating a vacuum and to produce a zero energy you have to fine tune the parameters. Previous work has indicated that the problem of finding a vacuum with a particular cosmological constant is NP hard. The energy of the vacuum is determined by summing the contribution of a large number of fields. Each field provides a positive or negative contribution and so the problem is finding a combination of fields that cancel to close to zero. This is where the number partitioning problem enters the picture. This problem requires that you split a very large collection of numbers into two sets of as close to equal size as possible. When you first encounter the problem is sounds easy, but when you try it out you quickly discover that it isn't so easy. In fact the problem is NP-hard - but there are some short cut methods that find a solution with a high probability in polynomial time. Solving the quantum field problem would take a long time, but the universe has already done it for us. In principle, we can make direct measurements of the fields and read off the solution that holds in our region of the universe. This thought prompts the researchers to posit a Computational Censorship Hypothesis: by physical measurements we must not be accessing the solution to a hard problem, i.e., a problem so hard that it could not have been solved by the physical resources in the observable universe. You can see the idea clearly - how can we access a result to a problem that is beyond the computational power of the universe? The estimate of the computational power of the universe does not allow it enough time to find the field settings for the cosmological constant by brute force search - and is thus a potential violation of the Computational Censorship Hypothesis. However, there are better algorithms. The Karmarkar-Karp heuristic, for example, allows a standard workstation to find a configuration in under 3 hours, which is well within the lifetime of the universe. The Karmarkar-Karp algorithm works by first sorting the numbers in the set into order and then dividing the numbers up by reading down the list and placing the value into alternate sets. This puts numbers that are as close in size as possible into different sets. Another way to look at this is to replace pairs of numbers in the sorted list by their difference - the final value being the difference between the two sets:
There are other clever algorithms that solve the problem with high probability in far less time than a brute force search. The research is part of an ongoing effort to combine complexity theory with physics in search of new computational principles. You can see some of the ideas in the following video presented by Stephen Jordan of the US National Institute of Standards and Technology:
What does all this mean? Does the universe use clever algorithms? You have to keep in mind that there is no workable theory of quantum gravity and this work makes use of a "toy" model from String theory. It is unlikely to apply in detail to the real universe, but it is an interesting approach to questions that we have hardly started answering. More InformationFast optimization algorithms and the cosmological constant Related ArticlesQuantum Physics Is Undecidable Microsoft Open Sources Quantum Computing Solve The Riemann Hypothesis With A Quantum Computer The Programmer's Guide to Chaos To be informed about new articles on I Programmer, sign up for our weekly newsletter, subscribe to the RSS feed and follow us on Twitter, Facebook or Linkedin.
Comments
or email your comment to: comments@i-programmer.info
|
|||
| Last Updated ( Saturday, 25 November 2017 ) |