| Amoeba Solves Traveling Salesman Problem |
| Monday, 28 December 2020 | |||
|
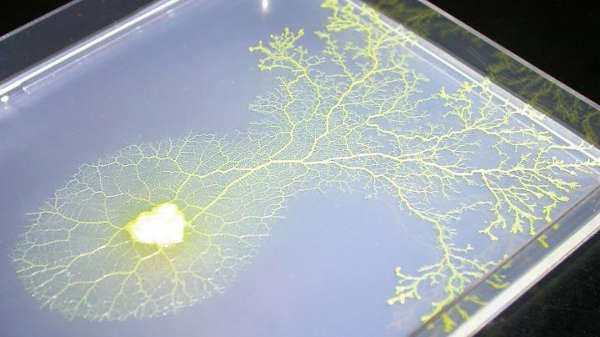
The traveling salesman problem is NP-hard so you really wouldn't expect a brainless amoeba to solve it - or would you? The Traveling Salesman Problem (TSP) is well-known to most programmers - given a list of cities find the shortest route that visits them all once, returning to the starting point. The only way of solving this problem is to try all possible paths to find the shortest and the number of paths that have to be tried increases exponentially, making the solution impossible for all but very small numbers of cities. If you can find a solution to the TSP problem in polynomial time, i.e. one that runs in a reasonable time for large numbers of cities, then you have a fast solution to a more restrictive form of the TSP problem. The more restrictive form is just answering the question "is that a path shorter than one given". This problem is in NP (Nondeterministic Polynomial) time - because if you give me a path that is proposed as being shorter then I can check this fact very quickly - just work out the length of the proposed shorter path. Notice that if I can solve TSP in polynomial time I can solve this restricted version of the problem in polynomial time. As this problem has also been shown to be NP complete we have also solved all problems in NP in polynomial time and hence have just won $1 million for proving that NP=P. So far no one has proved that NP=P or its converse. Every now and again someone invents an analog solution to the problem and sometimes suggests that this proves that NP=P. It doesn't and the reason why it doesn't is very obvious. For example consider the amoeba:
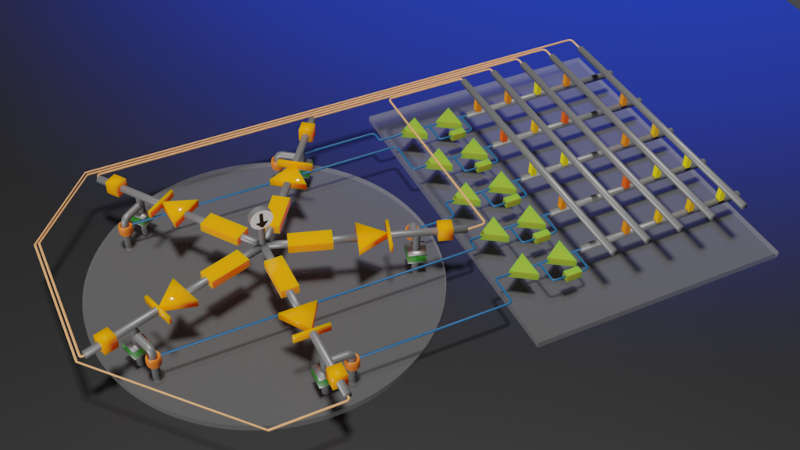
Photo: Masashi Aono "The amoeba is known to maximize nutrient acquisition efficiently by deforming its body. It has shown to find an approximate solution to the traveling salesman problem (TSP) ..." What this means is that if you put an amoeba on a substrate with nutrients spread out in a network of paths then it will grow to give you the shortest route between the points. This seems like an algorithm worth copying: This finding inspired Professor Seiya Kasai at Hokkaido University to mimic the dynamics of the amoeba electronically using an analog circuit, as described in the journal Scientific Reports. “The amoeba core searches for a solution under the electronic environment where resistance values at intersections of crossbars represent constraints and requests of the TSP,” says Kasai. Using the crossbars, the city layout can be easily altered by updating the resistance values without complicated pre-processing." This sounds interesting as it provides a simple and fast analog way of solving the TSP problem - which, apart from being important in computer science theory, is also of practical importance. "The system has high application potential, as it can determine a high-quality legal solution in a time that grows proportionally to the problem size without suffering from the weaknesses of Ising machines." The video below tells you a lot more about the biological system and the electronic implemenation: So is that NP=P solved? No - the electronic amoeba, like the real thing, only gives a good solution not the best possible solution to the problem. Solving TSP approximately isn't the same as solving it exactly for all cases in polynomial time. It may well turn out to be a practically useful method but it does nothing for theory. "This reliable and swift solution-searching capability could be beneficial for particular applications that prioritize the search time over the quality of a solution found. For example, in a situation at a disaster site where presenting reliable evacuation routes for residents is necessary, making a swift announcement should be prioritized than deriving the exactly optimal routes." Credit: Amoeba Energy
More InformationAmoeba‑inspired analog electronic computing system integrating resistance crossbar for solving the travelling salesman problem. Scientific Reports, November 27, 2020. Kenta Saito, Masashi Aono, Seiya Kasai Related ArticlesSlime mould simulates Canadian transport system To be informed about new articles on I Programmer, sign up for our weekly newsletter, subscribe to the RSS feed and follow us on Twitter, Facebook or Linkedin.
Comments
or email your comment to: comments@i-programmer.info <ASIN:1871962439> |
|||
| Last Updated ( Wednesday, 10 March 2021 ) |