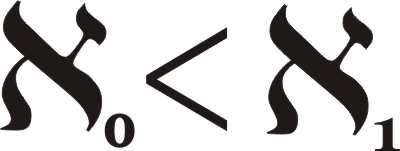| The Programmer's Guide To The Transfinite |
| Written by Mike James | |||
| Thursday, 25 January 2018 | |||
Page 2 of 2
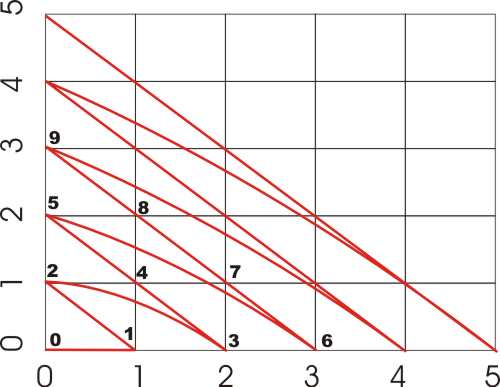
Is there an infinity bigger than the infinity of the integers? At first you might think that the rationals, i.e. numbers like a/b where a and b are integers, form a bigger set - but they don't. It is fairly easy, once you have seen how, to arrange a one-to-one assignment between integers and rational fractions. In fact it is easier and more general to consider the set (a,b) where a and b are natural numbers. If you have two sets A and B then the Cartesian product A X B of the two sets is the set of all pairs (a,b) with a taken from A and b taken from B. You can consider all the pairs (a,b) as the co-ordinates of a point in a grid with integer co-ordinates.
Now simply start at the origin and traverse the grid in a diagonal pattern assigning a count as you go: 0->(0,0), 1->(1,0), 2->(0,1), 3->(2,0), 4->(1,1) and so on. Clearly we have a one-to-one mapping of the integers to the co-ordinate pairs and so the co-ordinate pairs have the same order of infinity as the natural numbers. This also proves that the Cartesian product of two infinite sets is the same size. You can modify the proof slightly to show that the rationals a/b with b not equal to zero is also just boring standard infinite. Basically, if you can discover an algorithm that counts the number of things in a set, then that set is countable and an infinite countable set has order of infinity Aleph Zero. Two questions for you before moving on. Can you write a for loop that enumerates the point set (a,b) or equivalently give a formula i->(a,b)? Why do we have to do the diagonal enumeration? Why cant you just write two nested loops which count a from 0 to infinity and b from 0 to infinity? So what is bigger than Aleph Zero? Consider the real numbers, that is the rational numbers plus the irrationals. The reals are the set of infinite decimal fractions - you can use other definitions and get to the same conclusions. You also only have to consider the set of reals in the interval [0,1] to find a set that has more elements than the integers. How to prove that this is true? Cantor invented the diagonal argument for this and it has been used ever since to prover things like Godel's incompleteness theorem and more. It has become a basic tool of logic and computer science. To make things easy let's work in binary fractions. Suppose there is an enumeration that gives you all the binary fractions between 0 and 1. We don't actually care exactly what this enumeration is as long as we can use it to build up a table of numbers:
and so on. All we are doing is writing down the enumeration i -> a binary real number for i an integer.
If this enumeration exists then we have proved that there are as many reals as integers and vice versa and so the reals have an order of infinity that is aleph 0 i.e. they are countable. If this is all true the enumerations contains all of the reals as long as you keep going. If we can find a real number that isn't in the list then we have proved that it isn't a complete enumeration and there are perhaps more reals than integers. Now consider the following argument. Take the first bit after the binary point of the first number and start a new number with its logical Boolean Not - that is, if the bit is 0 use 1 and if it is 1 use 0. Next take the second bit from the second number and use its Not for the second bit of the new number. In fact you can see that the new number is simply the logical Not of the diagonal of the table. In this case:
This new number s is not equal to the first number in the table because it has been constructed to differ in the first bit. It is not equal to the second number because it has been constructed to be different in the second bit, and so on. In fact you can see that s differs in the nth bit after the binary point from the nth number in in the table. We have no choice to conclude that s isn't in the table and so there is a real number not in the supposedly complete enumeration - in other words there can be no such complete enumeration because if you present me with one I can use it to create a number that it doesn't include. You cannot count the real numbers and there are more real numbers than there are integers. Can you see why the argument fails if the fractions are not infinite sequences of bits? |
|||
| Last Updated ( Wednesday, 31 January 2018 ) |