Hashing is arguably one of the great ideas of computing and it has hidden depths. Extensible hashing and perfect hashing are ideas that are worth exploring.

What Programmers Know

Contents

1. The Computer - What's The Big Idea?*
2. The Memory Principle - Computer Memory and Pigeonholes*
3. Principles of Execution - The CPU
4. Assemblers and assembly language*
5. The Essence Of Programming
6. Variables - Scope, Lifetime And More*
7. Binary Arithmetic
8. Hexadecimal*
9. Binary - Negative Numbers*
10. Floating Point Numbers*
11. Inside the Computer - Addressing
12. The Mod Function
13. Recursion
14. The Lost Art Of The Storage Mapping Function *
15. Hashing - The Greatest Idea In Programming
16. Advanced Hashing
17. XOR - The Magic Swap*
18. Programmer's Introduction to XML
19. From Data To Objects*
20. What Exactly Is A First Class Function - And Why You Should Care*
21. Stacks And Trees*
22. The LIFO Stack - A Gentle Guide*
23. Data Structures - Trees
24. Inside Random Numbers
25. The Monte Carlo Method
26. Cache Memory And The Caching Principle
27. Data Compression The Dictionary Way
28. Dates Are Difficult*
29. Sequential Storage*
30. Magic of Merging*
31. Power of Operators
32. The Heart Of A Compiler*
33. The Fundamentals of Pointers
34. Functional And Dysfunctional Programming*

* Recently revised

When we covered the basics of hashing in Hashing - The Greatest Idea In Programming some exciting ideas were left out - extensible hashing and perfect hashing.

Don't be put off by the jargon because they are both simple and the sort of idea that you wish you'd thought of first. If you want to be reminded of what hashing is all about read the next section - Simple Hashing before continuing - otherwise skip to the next section.

Simple hashing

One of the most difficult things in computing is storing something where you can find it again.

The most obvious method is to store the data in sorted order and search using a binary search for example.

Hashing is a much more ingenious way of doing the same job.

All you need is a suitable hashing function

HASH(k)

say which will take the data value k, the key, and convert it into a storage location.

The data is then stored at the location and if you ever want it again you simply use HASH(k) to find it.

For example, to keep a list of names and addresses keyed on surname you might use a hash function which added together the ASCII values of each letter in the surname. The resulting sum could then be used as the index to an array of records used to store the name and address.

When you want the record again you simply hash the surname and go straight to the location where it is stored.

The only complication with hashing is that hash functions are imperfect and often send different keys to the same location. For example, two addresses with the different surnames might be mapped to the same array element.

This is called a collision and hashing methods vary in the way that they cope with the problem. Open hashing simply chains the collided items off the one array location so effectively storing them all at the same array index value as a linear list. Closed hashing uses a hashing function for a second time to give another location in the array where the item that caused the collision can be stored.

For an example of hashing and more on collisions see - Hashing - The Greatest Idea In Programming

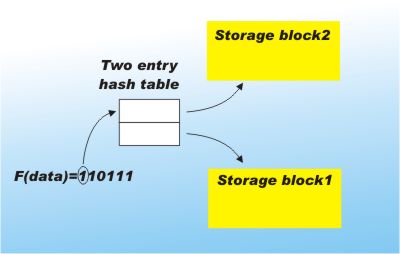
Extensible hashing

One of the practical difficulties with hashing is the way that the hash table has to be set up at a fixed size before any data is added to it.

The reason is that the hash function has to generate locations in the range 1 to M, where M is the size of the array used to form the hash table. (In practice this is usually achieved by taking the output of the hash function MOD M - see The Mod function.)

If you want to increase the size of the hash table then the amount of work involved is far too much. You would essentially have to re-hash every single item in the table!

There is a solution.

Extensible hashing is a technique that is particularly suited to storing data on disk. Instead of using the hash function to determine which exact location data is stored in, it is used to specify a fixed sized block of storage.

Each block will be used to store as many items as are hashed to it. At the moment this sounds just like a limited form of open hashing but there is more.

The trick is that while a full N-bit hashing function is computed, only the first few bits are actually used as an index to a table of blocks.

For example, if there are only two blocks in use then the index table will have only two entries which are selected using just the first bit of the hash result.

You can see that using this scheme on average half of the key values are stored in each block.