Do you know binary? There are only 10 possible answers and even if it's a 1 it's still fun to consider the wider concepts.

What Programmers Know

Contents

1. The Computer - What's The Big Idea?*
2. The Memory Principle - Computer Memory and Pigeonholes*
3. Principles of Execution - The CPU
4. Assemblers and assembly language*
5. The Essence Of Programming
6. Variables - Scope, Lifetime And More*
7. Binary Arithmetic
8. Hexadecimal*
9. Binary - Negative Numbers*
10. Floating Point Numbers*
11. Inside the Computer - Addressing
12. The Mod Function
13. Recursion
14. The Lost Art Of The Storage Mapping Function *
15. Hashing - The Greatest Idea In Programming
16. Advanced Hashing
17. XOR - The Magic Swap*
18. Programmer's Introduction to XML
19. From Data To Objects*
20. What Exactly Is A First Class Function - And Why You Should Care*
21. Stacks And Trees*
22. The LIFO Stack - A Gentle Guide*
23. Data Structures - Trees
24. Inside Random Numbers
25. The Monte Carlo Method
26. Cache Memory And The Caching Principle
27. Data Compression The Dictionary Way
28. Dates Are Difficult*
29. Sequential Storage*
30. Magic of Merging*
31. Power of Operators
32. The Heart Of A Compiler*
33. The Fundamentals of Pointers
34. Functional And Dysfunctional Programming*

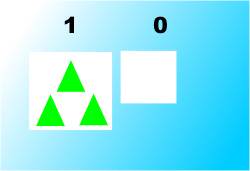
* Recently revised

What could be simpler than binary arithmetic? It’s just two-fingered counting and, once you know how it works, it seems natural for a computer to use it. But decimal is so built into our hands that it took quite a long time before we realized that two fingers were enough.

We are so used to counting and doing simple arithmetic that we tend to forget that if you don’t choose the right system then it all looks very difficult.  We also tend to think that the base ten place value system which is what we normally use is so natural it must be ... well, natural! Of course it isn't and there are lots of different ways of counting.

To understand the binary system let's first look at a system with more digits than just 0 and 1 and which used a mixed base.

The duo-decimal system

You might think that using a decimal place value system is so blindingly obvious that only an idiot would use anything else - but it isn’t that long since the UK dropped the mixed base duo-decimal monetary system,

The duo-decimal system is a good example of a mixed based system. This counted first in base 12 to get shillings, 12 pence makes one shilling, and then in base 20 to get pounds, 20 shillings makes one pound.

The imperial system of weights and measures still hangs on in both the USA and the UK and it’s even more eccentric. For example, weight is counted first to base 16 (ounces to pounds), then base 14 (pounds to stones) then base 8 (stones to cwt) and then base 20 (cwt to tons)!

So much for the attractive simplicity of the base ten place value system!

However this doesn’t mean that any old system of numbers works as well as any other. It has even been suggested that the Romans would have been better engineers if it wasn’t for their incredibly complicated mixed-base no-place value system.

Exactly how you count affects how easy it is to perform arithmetic and hence counting matters.

Base and place

So what is a “place value” system and how does it work?

The idea is that you first choose your base and arrange to have just enough symbols, any symbols you like, to count up to one less than this value.

For example, if you choose 3 as the base you need symbols for 0, 1, and 2 but you could just as easily use the symbols A, B and C. The symbols don't matter but in most cases we pick the traditional digits for values up to nine even though this risks confusion with a decimal system. 

Counting in base three leads quickly to a problem common to all counting systems that use a limited number of symbols.

What do you do when you get to 2 and need to count to 3? Remember you only have the symbols 0, 1 and 2.

The answer should be familiar to any digit-counting human - you make a group of three, i.e. 1 group of three and nothing extra,  which you write down as 10.

Notice that this is not “ten” but “one zero in base 3”.

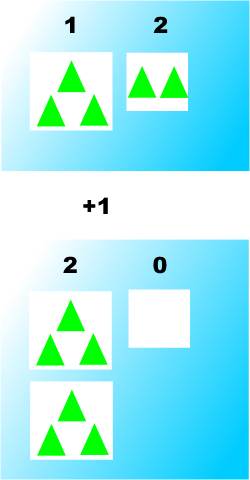
Then you carry on counting: 11 (i.e. 1 lot of 3 and 1), 12 (i.e. 1 lot of 3 and 2) and then you reach another group of 3.

So now you have two groups of 3 which you write down as 20 which is not “twenty” but “two zero in base 3”.

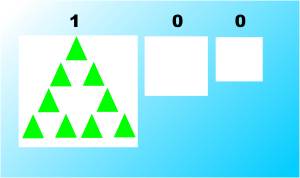
You carry on like this until you reach 22 and adding one more makes this into three groups of three which you write 100, which means that you have one group of three groups of three.

Think of it as a hierarchy in which you build a group of three things each of which is in turn a group of three things and so on.

We could go on labouring this idea all day - but now you either see what is going on or you are totally confused. If you are confused then go through the same steps with the base you know best, i.e. base 10, and see what happens.