| Say It With A Smile - Male Or Female |
| Written by Mike James | |||||||||||
| Sunday, 25 March 2018 | |||||||||||
|
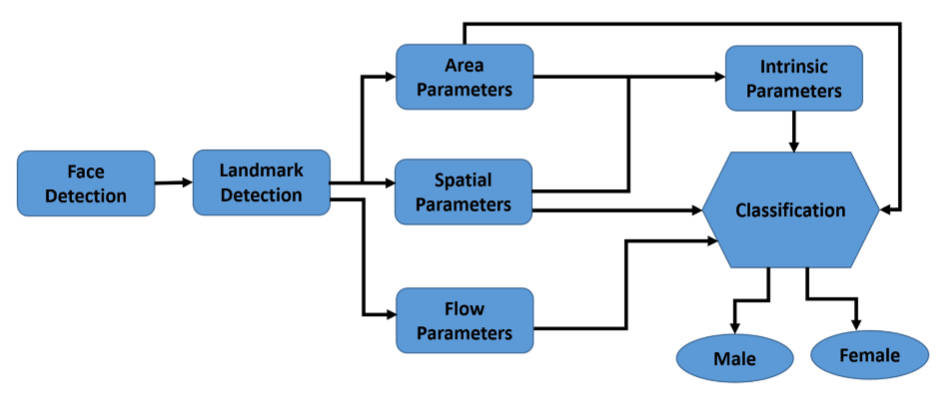
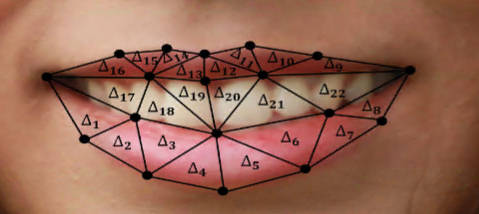
AI researchers have managed to predict if a subject is male or female just from the way they smile. This raises some interesting questions, but probably not the ones you are thinking of. Do males and females smile in different ways? Professor Hassan Ugail and Ahmad Al-dahoud from the Centre for Visual Computing, Faculty of Engineering and Informatics of Bradford University in the UK decided that the best way to find out would be to use machine learning to classify smiles. The problem was more difficult than you might think because they decided to use dynamic features. That is rather than just compare smiles at fixed points in time - maximum smile say - they decided to include features that depended on how the smile developed: "Our dynamic framework measures changes in the face during a smile using a set of spatial features on the overall face, the area of the mouth, the geometric flow around prominent parts of the face and a set of intrinsic features based on the dynamic geometry of the face. This enables us to extract 210 distinct dynamic smile parameters which form as the contributing features for machine learning." This was also implemented as an AI system:
The features are all hand constructed and establish a set that could be used in further work. The data sets used, and yes there are data sets of people smiling, consisted of 109 subjects - 69 females and 40 males.
A preliminary examination of the data features relating to smile area were compared only to show no obvious male/female differences. However when time is taken into account there did seem to be a difference: "Hence, it indeed confirms the smiles of females expand more through time in comparison to males." Using just this summary feature the classification accuracy was 60% which is only slightly above chance (50%). Moving on the team tried other machine learning techniques. SVM only achieved 69%, but a k-NN algorithm achieved 86% which led the researchers to conclude that males and females do smile differently. The results are reported in the April 2018 issue of Visual Computing and the article is also available on open access. Is this conclusion valid - 86% of a relatively small sample having hunted for a method that works, doesn't seem very impressive. In fact it seems to go against conventional statistical reasoning which says you should never select the analysis to just get the result you want. Once upon a time a gender difference question would have been taken to be a matter for statistics. Gather some data and perform a statistical test of the significance of the difference. However, what if, like a smile, the thing you wanted to test was complex? Why not simply construct a rule and see if it can successfully distinguish between the two groups. If it can, reliably, then there is a difference. If it only does as well as chance then there isn't, on the basis of the data you have used. This sort of exact approach seems to have been forgotten in the rise of "big data", "data science" and, to an extent, in AI and machine learning. This sort of reasoning is a question about the significance of the result, i.e. what is the probability of getting the result by chance alone. The problem we are looking at is sample size. Is a sample of 109 subjects with an 86% classification rate enough to be significant, i.e. rule out the possibility that this is just a chance occurrence. Interestingly you can compute the significance of a k-NN classifier result fairly easily. Imagine that the sample is from one distribution and the male/female labels have just been assigned randomly - i.e. there is no difference between male and female. Then what is the probability of getting a correct classification by chance alone? If you take a sample of n and then classify a new point from the same distribution what is the probability it lands next to a point with the same label? As the labels are applied randomly to the points the answer is obviously 0.5, assuming that the two groups are of equal size. When, as here, the two labels aren't equal then the probability is (1-p)^2+p^2, which makes it slightly more likely. Now if you repeat the classification for m points the probability of getting the correct classification of c points by chance alone is given by the cumulative binomial distribution (it is the same a tossing a coin m times and getting c heads). This argument works even if you use a cross validation method because this doesn't modify the argument about labels agreeing by chance alone (notice that in k-NN you always leave out the point being classifed anyway. So for example suppose we have a classifier based on a sample of N and a classification result of 86% what is the probability of getting this by chance alone:
You can see that for a sample size greater than 10 you have a significant result. Interestingly the first classification method tried only got 60% correct and the probably of getting this by chance alone is 0.186 which, as the researchers suggest, is not significant. For the smile data with a sample size of 109 the probability of getting 86% correct by k-NN classification by chance alone is vanishingly small and hence the result is significant, even allowing for trying multiple classification methods on the same data. So there is a difference in male and female smiles and the statistics backs up the machine learning. It would be intersting to see how an end-to-end training of a neural network would do on the same task.
More InformationRelated ArticlesYour tweets give away your gender To be informed about new articles on I Programmer, sign up for our weekly newsletter, subscribe to the RSS feed and follow us on Twitter, Facebook or Linkedin.
Comments
or email your comment to: comments@i-programmer.info |
|||||||||||
| Last Updated ( Sunday, 25 March 2018 ) |