| $30,000 For Rule 30 |
| Written by Mike James | |||
| Wednesday, 02 October 2019 | |||
|
Stephen Wolfram has just announced a prize for three proofs concerning Rule 30. What is Rule 30 and why is it so interesting? Cellular automata are very simple computing systems. You have a set of rules that are applied at each step and you watch initial configurations evolve. The best known example is the 2D Conway's Life, but Stephen Wolfram studied and classified a simpler 1D set of rules. The idea of a 1D CA is no different from a 2D one, but we start off with a line of cells and at the next tick the line is replaced by a new line determined by the rule that is being followed. As this is only a 1D arrangement, we don’t actually have to replace the existing line, just display the new line underneath, so building up a complete pattern of the development of the CA. It’s also possible to specify the rule in terms of the color of the cell, its two neighbors and the color of the new cell just below. For example the pattern:
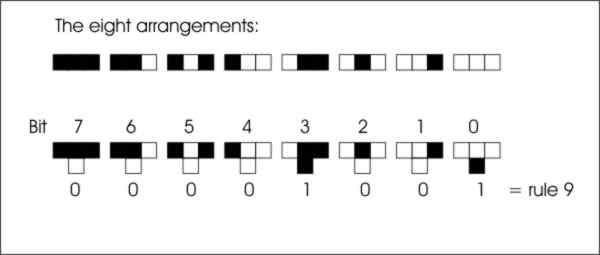
specifies a rule that if a cell is white and has two black neighbors then the cell below should be black. As there are only eight possible arrangements of neighbors, a complete rule that specifies exactly what should happen in any situation only has to list if the result of each of the eight is black or white. By thinking of black as 1 and white as 0 you can give each neighbor pattern a number between 0 and 7 and then read off the resulting black or white cell on the next row as a set of eight zeros or ones, i.e. a binary number. This can be used as an index to specify the rule.
This means you can refer to any of the 256 rules that are possible in a 1D CA by number. This in itself is something of a conceptual breakthrough, because now you can begin to think about classifying the behavior of each of the possible rules. Of all of the rules that we can look at, the most interesting is Rule 30, yes I know it is a shame it wasn't rule 42.
Rule 30 seem to produce a pseudo random pattern. Why is this interesting? Because complex behavior from such a simple rule is unexpected. This is what you get starting from a single black cell:
Yes there is regularity on the left, but on the right the pattern looks complex and it continues to evolve without repeats as the the number of generations increases. There are so many things we don't know about cellular automata and Wolfram has picked three theorems that need proofs for Rule 30. The prize is $10,000 for each one: Problem 1: Does the center column always remain non-periodic?In other words, can you prove that the center column never repeats or prove that it is eventually periodic. Computer simulation has already indicated that it doesn't become periodic after one billion steps. Problem 2: Does each color of cell occur on average equally often in the center column?If you compute the ratio of black to white cells this seems to converge to 1 as the number of generations increases, but is it exactly 1? Problem 3: Does computing the nth cell of the center column require at least O(n) computational effort?The direct way of computing the nth cell by simulation is O(n2), but is there a shortcut? It is surprising that not only isn't it clear how to even approach these problems, it also seems that we have little idea how difficult they are. It may take the invention of some new mathematical or computer techniques to even get a start. It might be that the solutions are obvious and all we need is some genius to look at the problems in a new way. You might not think that $10,000 is a lot for such a problem. It certainly isn't up there with the $1 million offered for the P=NP problem, but solve any of the rule 30 problems and people are going to take notice of you. Cellular automata have been proposed as the basis for a new physics, but the problem is we can't work with them. Answers to questions like these may push math and physics on to the next important theory. Details of the the prize and exactly what you have to do is on its web page and Wolfram has a blog post which fills you in on his thoughts on the matter and this makes essential reading if you are thinking about trying any of the problems. More InformationRelated ArticlesCellular Automata - The How and Why A New Computational Universe - Fredkin's SALT CA A Computable Universe - Roger Penrose On Nature As Computation SmoothLife - A Continuous Conway's Life To be informed about new articles on I Programmer, sign up for our weekly newsletter, subscribe to the RSS feed and follow us on Twitter, Facebook or Linkedin.
Comments
or email your comment to: comments@i-programmer.info |
|||
| Last Updated ( Thursday, 03 October 2019 ) |