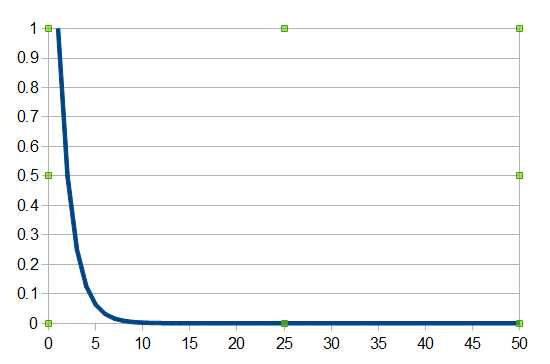
Kolmogorov Complexity Is Not Computable

The second difficulty inherent in the measure of Kolmogorov complexity is that, given a random-looking string, you can't really be sure that there isn't a simple program that generates it. This situation is slightly worse than it seems because you can prove that the Kolmogorov complexity of a string is itself a non-computable function. That is, there is no program (or function) that can take a string and output its Kolmogorov complexity. The proof of this, in the long tradition of such non-computable proofs, is proof by contradiction.

If you assume that you have a program that will work out the Kolmogorov complexity of any old string, then you can use this to generate the string using a smaller program and hence you get a contradiction. To see that this is so, suppose we have a function Kcomplex(S) which will return the Kolmogorov complexity of any string S. Now suppose we use this in an algorithm:

for I = 1 to infinity
 for all strings S of length I 
   if Kcomplex(S)> K then return S

You can see the intent, for each length of string test each string until its complexity is greater than K, and there seems like there is nothing wrong with this. Now suppose that the size of this function is N, then any string it generates has a Kolmogorov complexity of N or less. If you set K to N or any value larger than N you immediately see the problem. Suppose the algorithm returns S with a complexity greater than K, but S has just been produced by an algorithm that is N in size and hence string S has a complexity of N or less - a contradiction.

This is similar to the reasonably well known Berry paradox:

“The smallest positive integer that cannot be defined in fewer than twenty English words”

Consider the statement to be a program that specifies the number n which is indeed the smallest positive integer that cannot be defined in fewer than twenty English words. Then it cannot be the number as it has just been defined in 14 words. Notice that once again we have a paradox courtesy of self-reference. However, this isn't to say that all is lost.

Compressability

You can estimate the Kolmogorov complexity for any string fairly easily. If a string is of length L and you run it through a compression algorithm you get a representation which is L-C in length where C is the number of characters removed in the compression. You can see that this compression factor is related to the length of a program that generates the string, i.e. you can generate the string from a description that is only L-C characters plus the decompression program. 

Any string which cannot be compressed by even one character is called incompressible. There have to be incompressible strings because, by another counting argument, there are 2ⁿ strings of length n but only 2ⁿ-1 strings of length less than n. That is, there aren't enough shorter strings to represent all of the strings of length n.

Again we can go further and prove that most strings aren't significantly compressible, i.e. the majority of strings have a high Kolmogorov complexity. The theory says that if you pick a string of length n at random then the probably that it is compressible by c is given by 1-2^1-c+2^-n.

Plotting the probability of compressing a string by c characters for a string length of 50 you can see at once that most strings are fairly incompressible once you reach a c of about 5. 

Armed with all of these ideas you can see that a string can be defined as algorithmically random if there is no program shorter than it that can generate it - and most strings are algorithmically random.

In chapter but not in this extract

• Random and Pseudo Random
• Randomness and Ignorance
• Pseudo Random
• True Random

Summary

• The algorithmic, or Kolmogorov, complexity of a string of symbols is the size of the smallest program that will generate it.

• Kolmogorov complexity clearly depends on the machine used to host the program, but it is defined up to a constant which allows for the variation in implementation.

• Most irrationals don’t have programs that generate them and hence their Kolmogorov complexity is infinite.

• Kolmogorov complexity isn’t computable in the sense that there isn’t a single function or Turing machine that will return the complexity of an arbitrary string.

• A C compressible string can be reduced by C symbols by a compression program.

• A string that cannot be reduced by even one symbol is said to be incompressible. Such strings have to exist by a simple counting principle. This means that the majority of strings have a high Kolmogorov complexity.

• A string with a high Kolmogorov complexity is algorithmically random.

• Most random numbers are pseudo random in that they are theoretically predictable if not practically predictable. This includes examples of systems that are usually considered to be truly random, such as the toss of a coin. Clearly, with enough data, you can predict which face the coin will come down.

• The only example of true randomness is provided by quantum mechanics where the randomness is built into the theory – there is no way of predicting the outcome with more information.

A Programmers Guide To Theory

Now available as a paperback and ebook from Amazon.

Contents

1. What Is Computer Science?
   Part I What Is Computable?
2. What Is Computation?
3. The Halting Problem
4. Finite State Machines
   Extract 1: Finite State Machines
5. Practical Grammar
6. Numbers, Infinity and Computation
   Extract 1: Numbers 
   Extract 2: Aleph Zero The First Transfinite
   Extract 3: In Search Of Aleph-One
   Extract 4: Transcendental Numbers
   
7. Kolmogorov Complexity and Randomness
   Extract 1:Kolmogorov Complexity 
8. The Algorithm of Choice 
9. Gödel’s Incompleteness Theorem
10. Lambda Calculus ***NEW!
    Part II Bits, Codes and Logic
11. Information Theory 
12. Coding Theory – Splitting the Bit
13. Error Correction 
14. Boolean Logic
    Part III Computational Complexity
15. How Hard Can It Be?
    Extract 1: Where Do The Big Os Come From
16. Recursion
    Extract 1: What Is Recursion
    Extract 2: Why Recursion
17. NP Versus P Algorithms
    Extract 1: NP & Co-NP
    Extract 2: NP Complete

<ASIN:1871962439>

<ASIN:1871962587>

To be informed about new articles on I Programmer, sign up for our weekly newsletter, subscribe to the RSS feed and follow us on Twitter, Facebook or Linkedin.

Comments

Make a Comment or View Existing Comments Using Disqus

or email your comment to: comments@i-programmer.info