| Quadtrees and Octrees |
| Written by Mike James | ||||||
| Thursday, 09 August 2018 | ||||||
Page 2 of 2
The OctreeOnce you have understood the quadtree, the octree is almost obvious. In three dimensions the square is replaced by a cube and the division into four is replaced by a division into eight sub-cubes – hence oct–tree, since oct = eight.
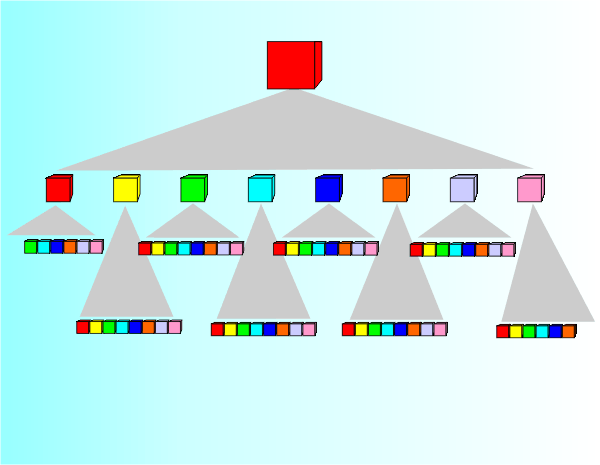
Thus the octree is just a generalization of the quadtree to 3D. Each node corresponds to a single cube and has exactly eight sub-nodes. Notice that all of the sub-node cubes are contained within the parent cube. As in the case of the quadtree, the octree can be used to find a data point, but this time a three-dimensional point, very quickly. As before you can flatten out the octree and draw it as a standard tree structure.
The octree branches very rapidly and it doesn’t take very many levels to generate lots of nodes but apart from this implementing it as a data structure isn't difficult. What tends to be difficult is managing the geometry needed to divide the cubes and store the details at each node. As in the case of the quadtree the octree is often built up dynamically as data become available. In this case dynamic construction often results in an unbalanced tree with areas of space being covered more finely than others. As already mentioned octrees are useful when you have to search a 3D space. In particular they are often used in efficient collision detection but they also occur in algorithms that work in more abstract 3D space. For example the color space is generally considered to be 3D with dimensions Red, Green and Blue. Hence you can use an octree to organise the use of color by an image and perform color reduction or quantization.
Related reading Donald Knuth's Christmas Tree Lecture Javascript data structures - the binary tree Data Structures Part I - From Data To Objects Data Structures Part II - Stacks And Trees To be informed about new articles on I Programmer, sign up for our weekly newsletter, subscribe to the RSS feed and follow us on Facebook or Linkedin.
<ASIN:0521106974> <ASIN:0201853922> <ASIN:3838329201> <ASIN:1420053361> <ASIN:1558607323> <ASIN:0262062178> |
||||||
| Last Updated ( Thursday, 09 August 2018 ) |
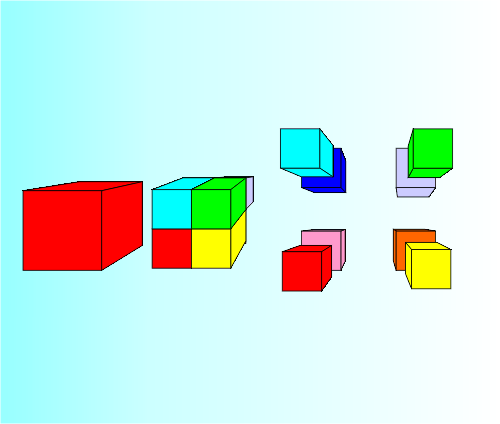 An octree division divides each cube into eight sub-cubes.
An octree division divides each cube into eight sub-cubes.