What is a Turing Machine?

Written by Mike James

Thursday, 23 November 2017

Article Index
What is a Turing Machine?
Universal Turing Machine

Page 2 of 2

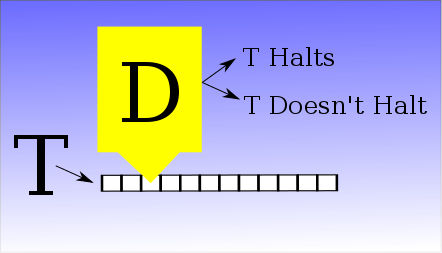
The Universal Turing Machine

Now we come to the masterstroke of Turing machine theory – the Universal Turing machine.

Suppose you have a Turing machine that computes something. It consists of a finite state machine, an initial state and an initialised tape.

These three things completely define the Turing machine.

The key idea in creating a Universal Turing machine is to notice that the information that defines a specific Turing machine can be coded onto a tape. The description of the finite state machine can be written first as a table of symbols representing states and transitions to states i.e. it is a lookup table for the next state given the current state and the input symbol. The initialisation information can then be written on the tape and the remainder of the tape can be blank and used as the Universal Turing machine’s tape.

Now all we have to do is to design a Turing machine that reads the beginning of the tape and uses this as a “lookup table” for the behaviour of the finite state machine. It can then use another special part of the tape to record the machine’s current state. It can read the symbols from the original machine’s initial tape, read the machine definition part of the tape to lookup what it should do next, and write the new state out to the working area.

What we have just invented is a Turing machine that can simulate any other Turing machine – i.e. a Universal Turing Machine.

Just in case you hadn’t noticed a universal Turing machine is just a programmable computer and the description on the tape of another Turing machine is a program.

The Universal Turing machine simulates any specific Turing machine in software.

What is computable?

At this point it all seems very reasonable – anything that can be computed can be computed by a specific Turing machine.

Even more generally, anything that can be computed can be computed by a Universal Turing machine a very particular Turing machine - by virtue of it being able to simulate any other Turing machine.

This all seems innocent but there is a hidden paradox waiting to come out of the machinery and attack – and again this was the reason Turing invented all of this!

Consider the “halting problem”.

This is just the problem of deciding if a given Turing machine will eventually halt on a specific tape.

In principle it looks reasonably easy.

You examine the structure of the finite state part of the machine and the symbols on its tape and work out if the result is halting or infinitely looping.

Given that we claim that anything that can be computed can be computed by a Turing machine let’s suppose that there is just such a machine called “D”. This machine will read the description of any Turing machine, “T”, and its initial data from its tape and will decide if T ever stops.

halt1

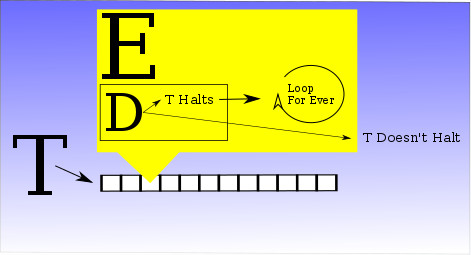
That is, you feed the tape that describes machine T to the machine D and it works for a while and then comes to a halt in one of two states that signal the result either “T Halts” or “T doesn’t Halt”.

Now we make a small change to the machine D to produce machine E – by adding two additional states L and R. These are arranged so that if machine D reaches the original “Halt” state it loops forever round L and R, no matter what is on the tape.

halt2

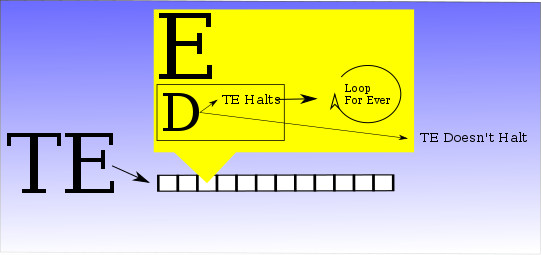
Notice that if machine D can be built so can machine E and this machine simply stops if machine T would never stop and never stops if machine T stops. That is machine E exhibits the opposite behaviour in terms of stopping to that of machine T.

All this seems innocent but you might notice the trap built into machine E.

Take machine E and create a tape TE which is a description of machine E suitable for a universal Turing machine. Now feed this tape into machine E itself and consider what will happen.

halt3

If machine E comes to a halt on tape TE this means that the machine described by TE does not halt – but wait a minute the machine described by TE is machine E!

Making this absolutely clear we have constructed a Turing machine that halts if and only if it doesn't halt!

If you try to wriggle the other way and say that machine E does not halt then this means that the tape describes a machine that does halt and again this machine is Turing machine E.

We have a machine that does not halt if it most certainly does!

A paradox.

At this point you probably want to start to pick your way through this explanation to find the flaw and I have to admit that I have cut a few corners in the interests of simplicity but you can trust me that any defects can be patched up without changing the overall paradox.

We are now left with the problem of interpreting these results and this isn’t so difficult. If machine D exists you can use it to construct a paradox and as paradoxes of this sort cannot exist – it is a “set of all sets” paradox – we have to conclude that machine D cannot exist.

In other words, it is impossible to build a Turing machine that can solve the halting problem – and given we believe that anything that can be computed can be computed by a Turing machine we now have the unpleasant conclusion that we have found a problem that has no solution.

We have found something that is beyond the limits of computation.

As soon as you have one the flood gates open and there are lots of non-computable problems – does machine T halt on input tape TT, does machine T ever print a particular symbol, does T ever stop when started on a blank tape and so on.

It is very important to note that hidden within all these descriptions is the use of the fact that a Turing machine has a finite but unbounded tape. For any Turing machine that has a fixed size tape the halting problem is solvable in theory.

Non-computable numbers

You can comfort yourself with the thought that these non-computable problems are a bit esoteric and not really practical – but there is more.

We are all very smug about the ability to compute numbers such as pi to millions of decimal places, it seems to be what computers were invented for.

The bad news is that there are non-computable numbers.

To see that this is the case, think of each Turing machine tape as being a number – simply read the binary number you get from a coding of its symbols on the tape that describes it to a Universal Turing machine.

So to each tape there is an integer and to each integer there is a tape. We have constructed a one-to-one numbering of all the possible Turing machines.

Now consider the number R which starts with a decimal point and has a 1 in decimal position n if the nth Turing tape represents a machine that halts when run on U, the universal Turing machine, and a 0 if it doesn’t halt.

Clearly there is no Turing machine that computes R because this would need a solution to the halting problem and there isn’t one… R is a non-computable number but again you can comfort yourself with the idea that it is a bit strange.

The really bad news is that it is fairly easy to prove that there are far more non-computable numbers than there are computable numbers.

Just think about how many real numbers there are and how many tapes – there is only a countable infinity of computable numbers as there is only a countable infinity of tapes but there is an uncountable infinity of real numbers in total. See: The Programmer's Guide To The Transfinite if you are unclear what countable and uncountable is all about but put even more simply - there are more real numbers than there are programs to compute them.

Most of the world is outside of our computing…

Halting

Alan Turing Year Starts Today