Ranking investments

The positive NPV rule works very well if you are only interested in making a yes or no decision about an investment.

What is more difficult is when there are a number of mutually exclusive investment opportunities and you have to choose just one to invest in.

This investment choice problem requires potential investments to be ranked in order of ‘quality’.

After our discussion of NPV and IRR these two quantities seem obvious candidates for ranking investment - however they both need to be used with care and understanding.

The main problem with the IRR is that it may not exist or may have multiple values. However when a single value does exist it still has a number of potential difficulties.

The first is a characteristic shared by all percentage measures. If have $10,000 and you are offered two investments one at 9% and one at 10% it is immediately obvious which is the best. Most people would accept the 10% investment without a moments thought.

However, if you are told that the two investments are mutually exclusive, i.e. you cannot accept both, but the 10% investment is limited to £100, you will begin to see that the situation isn’t quite so simple.

In this case the maximum profit from the 10% investment is limited to £10 per annum but the 9% investment is limited only by the capital you have at your disposal and is potentially worth much more.

You might think that this either/or situation is contrived and in practice you would be able to invest the first £100 in the 10% yielding investment and the residual in the 9% investment. This is generally true when the investment is of a purely financial nature, but when other resources are involved then this mutually exclusive behaviour is quite common.

For example, if the both investments make use of a limited resource - a machine, key personnel or management then you may very well have to choose between a 10% and 9% return on a pair of mutually exclusive projects.

To summarise

If there is no limit on the amount that can be invested then it is reasonable to rank potential investments by a percentage measure of return.

If there are limits on the amount invested in each case then percentage rankings can be misleading.

One way to think about this is realise that ranking investments by IRR say would favor an investment of £1 that made a return of £2 over more reasonably sized investments that offer a lesser rate!

If it is the total amount of the return that matters then mutually exclusive investments should be ranked by NPV. However, this is not to say that the ‘efficiency’ of the investment isn’t of concern. It is quite common to workout the ‘profitability index’ which is simply the NPV of the cashflow not including the initial investment divided by the initial investment. That is

PI = NPV(return cashflow)/investment

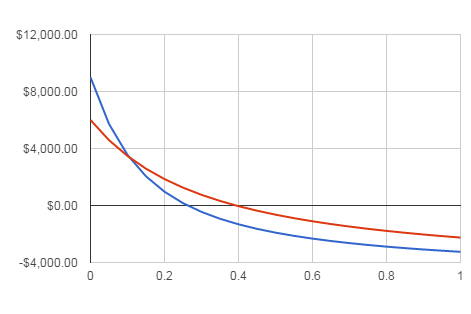
You should be able to see that the positive NPV rule is the same as accepting investments with a PI greater than 1.

This is fine, but as the PI is a relative measure of profitability it shares the problem of being a percentage measure when it comes to ranking mutually exclusive alternatives.

The PI index should be used as a measure of the efficiency of an investment but not as a way of choosing between mutually exclusive alternatives.

At this point you may think that the argument is all in favour of using the NPV as a way of ranking projects and this is in the main true.

However, you need to be aware of the way that NPV can change with different rates of interest. It is quite possible for the NPV to give different rankings depending on the interest rate chosen.

For example, consider the two NPV curves shown below:

For values of interest lower than 10% Project 1 (blue) has a higher NPV than Project 2 (red). However, for rates greater than 10% this ranking is reversed. This is a result of the of the former investment returning more money earlier than the other. 

Also notice that the IRR, i.e. where the lines cross the $0 axis, ranks Project 2 much higher than Project 1, even though for moderate interest rates Project 1 has a much higher return than Project 2.

This change in ranking isn’t an artifact but a true reflection of the changing desirability of each investment as the interest rate for a safe investment changes. Once again the NPV graph proves itself to be of more value than a simple index of worth.

<ASIN:1871962013>

<ASIN:B07S79ZVMQ>

<ASIN:0470178892>

<ASIN:0262046423>

<ASIN:1119067510>

<ASIN:078975584X>