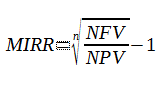The Modified IRR - MIRR

There have been a number of attempts to find a percentage measure of an investment's worth that does not have the failings of the IRR.

The most obvious modification to try to include is to apply different interest rates to the positive and negative cashflows.

One approach to doing this leads to the Modified Internal Rate of Return, which is often available to spreadsheet users as the MIRR financial function.

The key idea is that a reasonable definition of a rate of return is to compare the present value of all of the negative cashflows, i.e. the NPV, to the future value of the positive cashflows, i.e. the NFV. This reduces a complex investment to something that has just two events - an investment of the PV at the start and the receipt of the FV at the end. 

The standard relationship between the NFV and NPV is just:

NFV=NPV*(1+I)n

where n is the total number of periods in the project. 

Solving for I in this case gives the Modified Internal Rate Of Return, MIRR.

This all seems very reasonable and the MIRR has the advantage that it doesn't suffer from the IRR's tendency to have multiple values and it doesn't assume that all cash flows are subject to the IRR as interest rate for the life of the project. 

However, there are usually two interest rates that you do have to estimate.

When you compute the NPV and the NFV you have to assume an interest rate for each.

If you read the MIRR literature and examine examples, you will encounter long discussions about how to set these rates. It is usually suggested that the positive sums in the cashflow should be discounted by a reinvestment rate and the negative sums of money in the cashflow should be discounted by a finance interest rate i.e. the rate that money would be borrowed at.

However, if you think about the operational definitions of NPV and NFV, it is clear that a good choice is to set both rates to the interest rate that money can earn from a safe source.

For example, if a project needs you to invest S_i in the future, i.e. at period i, you can invest:

PVi = Si/(1+finance)^i

now which will grow to S_i at period i. So the finance rate should be set to the rate that you can get on a PV_i at the start of the project that gives you the amount you need to invest. In many cases this is the safe interest rate.

By the same reasoning, if  the investment generates S_i in the future this can be instantly reinvested at the reinvestment rate and this yields: 

FVi= Si*(1+reinvestment)(n-i) 

at the end of the investment.

Again, in many cases it is the safe investment rate that is appropriate.

The principle is clear - the finance rate should be the interest rate you can earn on a deposit when it isn't part of the project and the investment rate should be the interest rate you can earn on a deposit when it isn't part of the project. 

Notice that the MIRR reduces the importance of cash inputs and cash outputs that are late in the project. That is, spending money later in a project is good because it has a lower present value and receiving money early is good because it is available to reinvest. 

This description of how the MIRR is calculated can be summarised as:

1. Find the NPV of the negative part of the cashflow using the finance interest rate. This can be regarded as the present value of the total to be amount invested.
   
   
2. Find the NFV of the positive part of the cashflow using the reinvestment interest rate. This can be regarded as the future value of the total investment income.
   
   
3. Compute the MIRR using:

The MIRR isn't an easy calculation to do but most spreadsheets have a special MIRR function:

MIRR(cash flow range, finance rate, reinvestment rate)

For example if you compute the IRR for the cash flow shown in the previous spreadsheet:

IRR(B2:B14)

the IRR is 19% in agreement with the NPV diagram.

This makes the investment look very good against a 2% assumed safe rate. If we assume the finance and the reinvestment rate is 2% the MIRR can be calculated using:

=MIRR(B2:B14,2%,2%)

which works out to 12% which is still better than the safe rate, but not quite as promising.

The MIRR is a controversial topic in finance and most people prefer the NPV or the IRR. However, the MIRR is very realistic in that it relates what you have to invest now to what you will receive at a point in the future. It reduces all cash flows to the start and end of the project and as long as you understand the way that this works you can set the finance and reinvestment interest rates to something that suits your situation.  

To be informed about new articles on I Programmer, sign up for our weekly newsletter, subscribe to the RSS feed and follow us on Twitter, Facebook or Linkedin.

Comments

Make a Comment or View Existing Comments Using Disqus

or email your comment to: comments@i-programmer.info

<ASIN:1871962013>

<ASIN:B07S79ZVMQ>

<ASIN:0470178892>

<ASIN:0262046423>

<ASIN:1119067510>

<ASIN:078975584X>