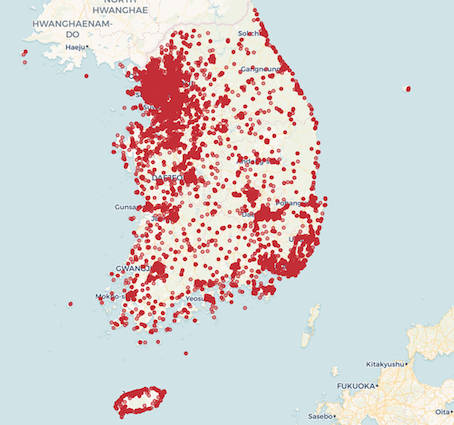
It is a truth universally acknowledged that the Travelling Saleman Problem (TSP) is impossible to solve for even reasonably small examples using today's computers. Do we need powerful hardware or a quantum computer? 

No, we just need a clever algorithm.

I can remember being advised not to try to implement a route planning program because it is well known that the TSP is impossible to solve. I should have stuffed my ears with cheese and got on with the task as so many sat nav and other route finders have since proved the lie to the assertion.

Even so, news that the shortest walking tour to 81,998 bars in South Korea has not only been found but is also proven to be the optimum solution, is slightly mind boggling. After you have recovered from the fact that there are 81,998 bars in South Korea, you can contemplate the temptation to go and open two more before starting to solve the problem.

The reason that the TSP is so difficult is that the number of possible solutions grows very rapidly with the number of bars. Just 2 bars and you have 1 path, 3 and you still have just 1 path, 4 and you have 3 paths and so on. It all seems very manageable and slow growing, but when you hit 20 bars you have 60,822,550,204,416,000 possible paths - clearly making a brute force examination of every path impractical. 

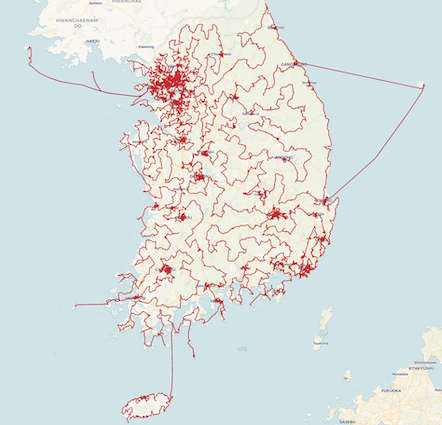
The bars

Now a team hosted by the University of Waterloo, but with many different affiliations, has constructed the shortest walking path between  81,998 bars and it has 2 followed by 367308 zeros possible paths. The first thing to say that the data was obtained from a database maintained by the Korean National Police Agency - which suggests that we should look more creatively for sources of experimental data.

So how was it solved?

The simple answer is using clever optimization algorithms. Normally an optimization algorithm can only give you an approximate solution but in this case using a "cutting plane method" generated dynamic estimates of how good the result was. The result is a solution that can be proven to be the best. You can look at the exact form of the algorithm in the announcementt of the result. What matters is that we have yet another example of an NP Hard problem not being that hard after all. To quote the Washington Post, not alone in its opinion:

"It would take a laptop computer 1,000 years to compute the most efficient route between 22 cities, for example."

and then it goes on to suggest that the solution is to use a quantum computer. Well perhaps not.

The optimum bar crawl

There is so much life in the study of algorithms that we might not need the power of a quantum computer to do impossible things.

•  Mike James is the author of The Programmer’s Guide To Theory which, as its subtitle "Great ideas explained" suggests, sets out to present the fundamental ideas of computer science in an informal and yet informative way. TSP is, of course, one of the topics covered in this popular book.

More Information

https://www.math.uwaterloo.ca/tsp/korea/index.html

Related Articles 

Neural Networks Take On Traveling Salesman

Amoeba Solves Traveling Salesman Problem

The Physical Travelling Salesman Challenge

Programmer's Guide To Theory - NP & Co-NP

NP-Complete - Why So Hard?

Minimum Spanning Tree

Computational Complexity

The XY Traveling Salesman Problem Solved

Traveling Salesman Applied To DNA Synthesis

To be informed about new articles on I Programmer, sign up for our weekly newsletter, subscribe to the RSS feed and follow us on Twitter, Facebook or Linkedin.

Comments

Make a Comment or View Existing Comments Using Disqus

or email your comment to: comments@i-programmer.info