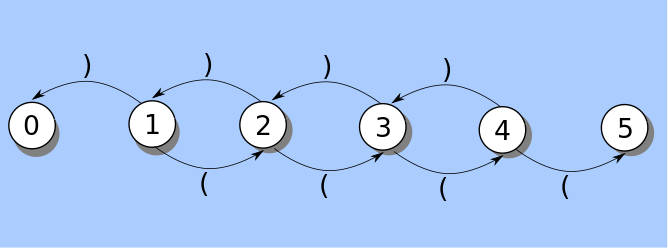
This algorithm is an example of Turing thinking. The algorithm ignores any issue of what resources are needed. It is assumed that pushes and pops will never fail for lack of resources. The algorithm is a Turing machine style unbounded algorithm that will deal with a string of any size.

Now consider a finite machine approach to the same problem. We need to set up some states to react to each ( and each ) such that if the string is balanced we end in a final state. In the machine below we start from state 1 and move to new states according to whether we have a left or right parenthesis. State 5 is an error halt state and state 0 is an unbalanced halt state.

Consider (())()

(())()		state 1 → state 2
())() 		state 2 → state 3
))()  		state 3 → state 2
)()   		state 2 → state 1
()		state 1 → state 2
)		state 2 → state 1

and as we finish in state 1, the string is balanced.

(()))(		state 1 → state 2
()))(		state 2 → state 3
)))(		state 3 → state 2
))(		state 2 → state 1
)(		state 1 → state 0

as we finish in state 0, the string is unbalanced.

Finally consider:

(((())))	state 1 → state 2
((())))	state 2 → state 3
(())))		state 3 → state 4
())))     	state 4 → state 5

as we finish in state 5, an out of memory error has occurred.

The difference between the two approaches is that one doesn’t even think about resources and uses the pattern in the data to construct an algorithm that can process any amount of data given the resources. The second deals with a problem with an upper bound – no more than four left parentheses can be processed.

Of course, this distinction is slightly artificial in that we could impose a bound on the depth of the stack and include a test for overflow and stop the algorithm. Would this be finite state thinking or just Turing thinking with a fix for when things go wrong? The point is that we construct pure algorithms that tend not to take resource limitations into account – we think Turing, even if we implement finite state. There is also a sense in which Turing thinking captures the abstract essence of the algorithm that goes beyond a mere mechanism to implement it.

The human mind can see algorithms that always work in principle even if in practice they have limits. It is the computer science equivalent of the mathematician conceiving of a line as having no thickness, of a perfect circle or indeed something that has no end.

Summary

• The finite state machine is simple and less powerful than other machines with unbounded storage such as the Turing machine.

• Finite state machines accept sequences generated by a regular grammar.

• Regular expressions found in most programming languages are a practical implementation of a regular grammar.

• The pushdown machine is slightly more powerful than a finite state machine and it accepts sequences generated by a context-free grammar.

• A full Turing machine can accept sequences generated by a phrase structured grammar.

• The different types of machine and grammars form a hierarchy of increasingly complex languages.

• Although a Turing machine is more powerful than a finite state machine, in practice all machines are finite state machines.

• A Turing machine with a tape limited to n cells is equivalent to a finite state machine with sⁿxwhere s is the number of symbols it uses and x is the number of states in its controller.

• Even though Turing machines are an abstraction and do not exist, we tend to create algorithms as if they did, making no assumptions about resource limits. If we do think of resource limits they are afterthoughts bolted on to rescue our inherently unbound algorithms.

• Algorithms that are unbounded are the pure thought of computer science.

A Programmers Guide To Theory

Now available as a paperback and ebook from Amazon.

Contents

1. What Is Computer Science?
   Part I What Is Computable?
2. What Is Computation?
3. The Halting Problem
4. Finite State Machines
   Extract 1: Finite State Machines
   Extract 2: Turing Thinking ***NEW!
5. Practical Grammar
6. Numbers, Infinity and Computation
   Extract 1: Numbers 
   Extract 2: Aleph Zero The First Transfinite
   Extract 3: In Search Of Aleph-One
   Extract 4: Transcendental Numbers
   
7. Kolmogorov Complexity and Randomness
   Extract 1:Kolmogorov Complexity 
8. The Algorithm of Choice
9. Gödel’s Incompleteness Theorem 
10. Lambda Calculus
    Part II Bits, Codes and Logic
11. Information Theory 
12. Splitting the Bit 
13. Error Correction 
14. Boolean Logic 
    Part III Computational Complexity
15. How Hard Can It Be?
    Extract 1: Where Do The Big Os Come From
16. Recursion
    Extract 1: What Is Recursion
    Extract 2: Why Recursion
17. NP Versus P Algorithms
    Extract 1: NP & Co-NP
    Extract 2: NP Complete

<ASIN:1871962439>

<ASIN:1871962587>

To be informed about new articles on I Programmer, sign up for our weekly newsletter, subscribe to the RSS feed and follow us on Twitter, Facebook or Linkedin.

Comments

Make a Comment or View Existing Comments Using Disqus

or email your comment to: comments@i-programmer.info