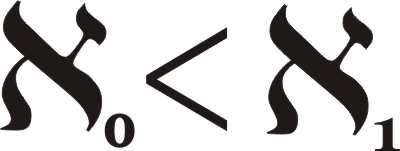| Programmer's Guide To Theory - In Search Of Aleph-One |
| Written by Mike James | |||||||
| Monday, 25 January 2021 | |||||||
Page 3 of 3
Aleph-One and BeyondThe size of the real numbers is called aleph-one and it is the size of the continuum – that model of space where between each point there is not only another point but an infinity of points. Aleph-zero is the sort of infinity we usually denote by ∞ and so aleph-one is bigger than our standard sort of countable infinity. This all seems a little shocking - we now have two infinities. You can show that aleph-one behaves in the same way as aleph-zero in the sense that you can take any lots of elements away, even aleph-one elements, and there are still aleph-one elements left. After the previous discussion, you can also see why the reals are not effectively enumerable and lead to a new order of infinity – they need two infinite loops. Of course, the problem with these loops is that the inner loop never ends so the outer one never gets to step on to the next real number in the enumeration. This raises the question of what we did to get from aleph-zero to aleph-one and can we repeat it to get to aleph-two? The answer is yes. If two sets A and B are aleph-zero in size then we already know that all of the usual set operations A U B, i.e. set A union B, is everything in both sets – often said as an infinity plus an infinity is the same infinity - and A X B all of the pairs obtained by taking one from A and one from B (the Cartesian product) for example also have aleph-zero elements. However, there is another operation that we haven't considered - the power set. If you have a set of elements A, then the power set of A, usually written 2A, is the set of all subsets of A including the empty set and A. So if A={a,b} the power set is {0,{a},{b}, A}. You can see why it is called the power set as a set with two things in it gives rise to a power set with four things, i.e. 22=4. This is generally true and if A has n elements its power set has 2n elements. Notice that this is a much bigger increase than other set operations, i.e A U A has 2n elements and A X A has n2 elements. The power set really does seem to change gear on the increase in the number of elements. So much so that if A has aleph-zero elements then it can be proved that 2A, i.e. the power set, has aleph-one elements. And, yes, if A has aleph-one elements its power set has aleph-two elements, and so on.
Notice also that the reals, R, are related to the power set of the integers, just as the rationals, Q, are related to the Cartesian product of the integers, i.e. R=2Z and Q=Z X Z with suitable definitions and technical adjustments. The set of alephs is called the transfinite numbers and it is said that this is what sent Cantor crazy but you should be able to see that it is perfectly logical and there is no madness within. So finally, are there aleph-zero, i.e. a countable infinity, of transfinite numbers or are there more? The answer is we don't know and it all hinges on the answer to the question "is there a set with an order of infinity between aleph-zero and aleph-one". That there isn't is the so-called continuum hypothesis, and it forms Hilbert's 23rd problem and here we get into some very deep mathematics and an area of active research. In book but not in this extract:
Summary
A Programmers Guide To Theory
Now available as a paperback and ebook from Amazon.
Contents
Bonus Chapter: What Would P=NP Look Like? ***NEW!
<ASIN:1871962439> <ASIN:1871962587> To be informed about new articles on I Programmer, sign up for our weekly newsletter, subscribe to the RSS feed and follow us on Facebook or Linkedin.
Comments
or email your comment to: comments@i-programmer.info |
|||||||
| Last Updated ( Monday, 25 January 2021 ) |